Introducción
Definición. Un árbol AVL es un árbol binario de búsqueda que cumple con la condición de que la diferencia entre las alturas de los subárboles de cada uno de sus nodos es, como mucho 1.
La denominación de árbol AVL viene dada por los creadores de tal estructura (Adelson-Velskii y Landis).
Recordamos que un árbol binario de búsqueda es un árbol binario en el cual cada nodo cumple con que todos los nodos de su subárbol izquierdo son menores que la raíz y todos los nodos del subárbol derecho son mayores que la raíz.
Recordamos también que el tiempo de las operaciones sobre un árbol binario de búsqueda son O(log n) promedio, pero el peor caso es O(n), donde n es el número de elementos.
La propiedad de equilibrio que debe cumplir un árbol para ser AVL asegura que la profundidad del árbol sea O(log(n)), por lo que las operaciones sobre estas estructuras no deberán recorrer mucho para hallar el elemento deseado. Como se verá, el tiempo de ejecución de las operaciónes sobre estos árboles es, a lo sumo O(log(n)) en el peor caso, donde n es la cantidad de elementos del árbol.
Sin embargo, y como era de esperarse, esta misma propiedad de equilibrio de los árboles AVL implica una dificultad a la hora de insertar o eliminar elementos: estas operaciones pueden no conservar dicha propiedad.
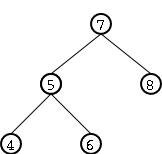
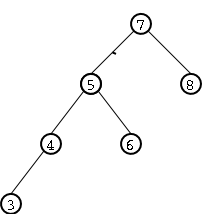
A modo de ejemplificar esta dificultad, supongamos que al árbol AVL de enteros de Figure 1 le queremos agregar el entero 3. Si lo hacemos con el procedimiento normal de inserción de árbols binarios de búsqueda el resultado sería el árbol de Figure 2 el cual ya no cumple con la condición de equilibrio de los árboles AVL dado que la altura del subárbol izquierdo es 3 y la del subárbol derecho es 1.
En the Section called Rotaciones simples se pasará a explicar una serie de operaciones sobre los nodos de un árbol AVL con las cuales poder restaurar la propiedad de equilibrio de un árbol AVL luego de agregar o eliminar elementos.
Declaración del tipo de dato
Iremos ya declarando el tipo de dato que representará un árbol AVL. Esto nos ayudará a formalizar las cosas y nos permitirá en el correr de este documento ir definiendo las operaciones sobre el tipo de dato abstracto.
El lenguaje a utilizar será C. Fue elegido tan sólo por gustos personales del autor de este documento. Sin embargo se tratará de usar sólo aquellas características de C que puedan ser fácilmente implementadas en la mayoría de los lenguajes estructurados como Pascal, Modula-2, etc.
Algunas consideraciones sobre la implementación del tipo de dato abstracto
Las declaraciones que se listarán a continuación no tienen porqué tomarse al pie de la letra. Cada programador tendrá su estilo y su forma de resolver sus problemas.
Las declaraciones que se listarán a continuación no tienen porqué tomarse al pie de la letra. Cada programador tendrá su estilo y su forma de resolver sus problemas.
Como se podrá ver en el siguiente listado, la única diferencia de los nodos de un árbol AVL con los de un árbol binario común es la variable altura en la estructura nodo.
Los nodos de un árbol pueden almacenar cualquier tipo de dato, arbitrariamente complejo. En este documento, por razones de simplicidad se usará el tipo de dato más simple que soporte comparaciones, o sea los enteros (tipo int de Ansi C). En el caso de que los datos almacenados en cada nodo sean más complicados (por ejemplo estructuras) o sean dinámicamente almacenados en memoria, algunas funciones deberán adaptarse para manejarlos. Por ejemplo, se deberá pasar como parámetros funciones de comparación, equivalencia, y de liberación de memoria.
A continuación se lista la declaración del tipo abstracto de dato Árbol AVL:
typedef struct AVLNode AVLTree;
struct AVLNode
{
int dato;  AVLTree izq;
AVLTree der;
int altura;
AVLTree izq;
AVLTree der;
int altura;  };
};

- Como ya dijimos, por cuestiones de simplicidad, la información almacenada en cada nodo del árbol será un entero.

- Cada nodo tendrá almacenada su propia altura con respecto a la raíz absoluta del árbol con el que estamos trabajando. Esta característica se verá en the Section called Consideraciones sobre la altura de los nodos.
A continuación declaramos las operaciónes básicas sobre árboles binarios y con las cuales trabajaremos para acceder al tipo abstracto de dato Árbol AVL de aquí en más.
Note: Si se usa algún lenguaje orientado a objetos como C++ o java y ya se tienen clases como árboles binarios o árboles binarios de búsqueda, conviene declarar los árboles AVL como una subclase de alguna de estas. Luego, las operaciones declaradas a continuación se heredarán de estos tipos.
/* Constructores */ AVLTree *vacio (void); /* devuelve un árbol AVL vacío */ AVLTree *hacer (int x, AVLTree * izq, AVLTree * der); /* devuelve un nuevo árbol formado por una raíz con valor x, subárbol izquierdo el árbol izq y subárbol derecho el árbol der. */ /* Predicados */ bool es_vacio (AVLTree * t); /* devuelve true sii. t es un árbol vacío. */ /* Selectores */ AVLTree *izquierdo (AVLTree * t); /* devuelve el subárbol izquierdo de t. */ AVLTree *derecho (AVLTree * t); /* devuelve el subárbol derecho de t. */ int raiz (AVLTree * t); /* devuelve el valor de la raíz del árbol t. Precondición: !es_vacio(t) */ int altura (AVLTree * t); /* devuelve la altura del nodo t en el árbol */ /* Destructures */ void destruir (AVLTree * t, void (*free_dato) (int)); /* libera la memoria ocupada por los nodos del árbol. Si los datos almacenados en cada nodo están almacenados dinámicamente y se los quiere liberar también, debe pasarse como segundo parámetro una función de tipo void func(int t) que libere la memoria de objetos int. Si los datos no están almacenados dinámicamente o simplemente no se los quiere destruir (liberar de memoria), pásese como segundo parámetro NULL. Nota: Función Recursiva! */
Note: Como se ha podido apreciar en el segmento de código anterior, se ha tratado de usar, en lo posible, el lenguaje español tanto para los comentarios como para los identificadores de variables y funciones. Sin embargo, esto se hace sólo con motivo de ser coherentes con el documento y el autor recomienda a los lectores programadores que en sus programas utilicen el lenguaje inglés para nombrar los identificadores.
Consideraciones sobre la altura de los nodos
Como vimos en la definición del tipo abstracto para nodos de árboles AVL, se necesitará tener acceso a la altura cada nodo del árbol en tiempo constante. Dado que una función para hallar la altura de un nodo dado en un árbol tendrá un tiempo de ejecución de O(log(n)) peor caso, no nos queda otra alternativa que almacenar una variable altura en cada nodo e irla actualizando en las inserciones y eliminaciones que se efectúen sobre el árbol.
Como el lector ya debería saber, una función para calcular la altura de un nodo puede escribirse recursivamente como:
int altura(AVLTree *t)
{
if(es_vacio(t))
return -1;
else
return max(altura(izquierdo(t)), altura(derecho(t)));
}Queremos que la altura de un árbol que consta de sólo un nodo sea 0. Entonces debemos definir la altura de un árbol vacío como -1.
Sin embargo, no podemos darnos el lujo de tener una función cuyo tiempo de ejecución siempre es O(n) ya que, como dijimos, necesitamos la altura de un nodo en tiempo constante. Para ello, redefiniremos la función de la siguiente manera, aprovechando el campo altura que ahora tiene cada nodo del árbol.
int altura (AVLTree * t)
{
if(es_vacio(t))
return -1;
else
return t->altura;
}Important: Debemos tener mucho cuidado en actualizar el campo altura de cada nodo siempre que modifiquemos de alguna manera el árbol AVL.
Así, es importante tener una función que nos permita actualizar la altura de un nodo cualquiera del árbol y cuyo tiempo de ejecución sea O(1) en el peor de los casos. A continuación se lista una tal función:
void
actualizar_altura (AVLTree * t)
{
if(!es_vacio(t))
t->altura = max (altura ((t)->izq), altura ((t)->der)) + 1;
}Rotaciones simples
Veremos a continuación una operación sencilla sobre un árbol binario de búsqueda que conserva el órden en sus nodos y que nos ayudará a restaurar la propiedad de equilibrio de un árbol AVL al efectuar operaciones sobre el mismo que puedan perturbarla.
Miremos por un momento el árbol de Figure 3. Dado que este es un árbol de búsqueda se debe cumplir x < y y además todos los nodos del subárbol A deben ser menores que x y y; todos los nodos del subárbol B deben ser mayores que x pero menores que y; y todos los nodos del subárbol C deben ser mayores que y y por lo tanto que x.
En Figure 4 se ha modificado sencillamante el árbol. Como puede verificarse fácilmente por las desigualdades descriptas en el párrafo anterior, el nuevo árbol sigue manteniendo el órden entre sus nodos, es decir, sigue siendo un árbol binario de búsqueda. A esta transformación se le denomina rotación simple (o sencilla).
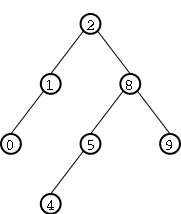
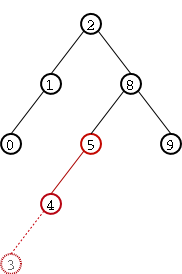
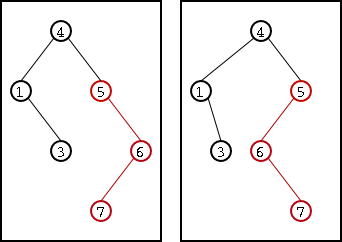
Veamos un ejemplo concreto. Deseamos insertar el número 3 en el árbol de enteros de Figure 5. La inserción se muestra punteada en Figure 6. Sin embargo, como puede verse, la inserción a provocado la pérdida de la propiedad de equilibrio del árbol ya que dicha propiedad no se cumple en el nodo marcado con rojo. ¿Qué hacemos para recomponer dicha pripiedad? Simplemente realizamos una rotación simple. En este caso se dice que la rotación es izquierda ya que la "pérdida de equilibrio se produce hacia la izquierda. En Figure 7 puede verse el árbol luego de la rotación: la propiedad de equilibrio ha sido reestablecida. Como mostramos atrás, la rotación conserva el orden entre los nodos, por lo que podemos afirmar que este último árbol si es AVL.
Figure 7. Reestablecimiento de la propiedad de equilibrio mediante una rotación simple sobre el nodo de valor 5.
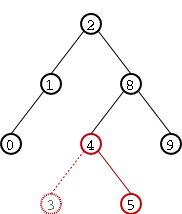
Como podemos observar, el resultado luego de la rotación es un árbol AVL: posee tanto el órden correcto de un árbol de búsqueda entre sus nodos y la propiedad de equilibrio. En este caso el "desequilibrio" en el árbol con raíz 5 era enteramente hacia la izquierda y por lo tanto, como ya dijimos, la rotación efectuada se denomina rotación simple izquierda. En el caso de un "desequilibrio" hacia la derecha, la rotación es análoga y se denomina rotación simple derecha. En Figure 8 se ven dos árboles: el primero tiene un "desequilibrio hacia la derecha" marcado en rojo y el segundo es el resultado de aplicar una rotación simple derecha.
Figure 8. Ejemplo de reestablecimiento de propiedad de equilibrio gracias a una rotación simple derecha.
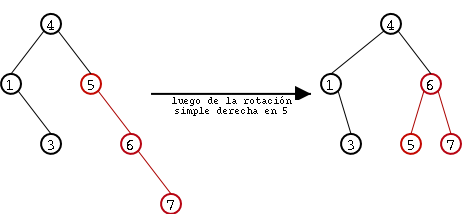
Ilustración de la operación rotación simple. en Figure 9 se ilustra la operación rotación simple. Los arcos de colores son los que se eliminan o agregan, según sea la rotación izquierda o derecha.
Implementación de la rotación simple:
void rotar_s (AVLTree ** t, bool izq);/* realiza una rotación simple del árbol t el cual se
pasa por referencia. La rotación será izquierda sii. (izq==true) o será derecha sii. (izq==false). Nota: las alturas de t y sus subárboles serán actualizadas dentro de esta función! Precondición: si (izq==true) ==> !es_vacio(izquierdo(t)) si (izq==false) ==> !es_vacio(derecho(t)) */ void rotar_s (AVLTree ** t, bool izq)

{ AVLTree *t1; if (izq) /* rotación izquierda */ { t1 = izquierdo (*t); (*t)->izq = derecho (t1); t1->der = *t; } else /* rotación derecha */ { t1 = derecho (*t); (*t)->der = izquierdo (t1); t1->izq = *t; } /* actualizamos las alturas de ambos nodos modificados */ actualizar_altura (*t); actualizar_altura (t1); /* asignamos nueva raíz */ *t = t1; }

- Declaración de la función rotar_s(). Esta declaración y el siguiente comentario deberían ir en el archivo de cabecera, interfaz del tipo abstracto árbol AVL con el usuario.

- Un breve comentario que explica lo que hace la función, los parámetros que acepta y las precondiciones que éstos deben cumplir para que la función se ejecute correctamente.

- Como el programador de C más experimentado puede ver, el paso a la función es el paso por referencia clásico en C. Lo que se pasa no es un puntero a la raiz del árbol sino la dirección de dicho puntero. De esta manera, dentro de la función podremos cambiar la misma raiz si es necesario (lo que justamente hacemos en las rotaciones).

- También se acepta como segundo parámetro un valor boleano que determina si la rotación simple a efectuar sobre el árbol es izquierda o derecha.
Rotaciones dobles
Hemos visto cómo restaurar la propiedad de equilibrio cuando se presentan desequilibrios "hacia la izquierda" o "hacia la derecha" luego de realizar inserciones en un árbol AVL. Sin embargo y como veremos, pueden ocurrir "desequilibrios en zig-zag", es decir desequilibios que no son ni a la derecha ni a la izquierda como es el caso de los árboles de Figure 10.
En estos casos se aplica otro tipo de rotación denominado rotación doble la cual, análogamente a la rotación simple, puede ser izquierda o derecha según el caso.
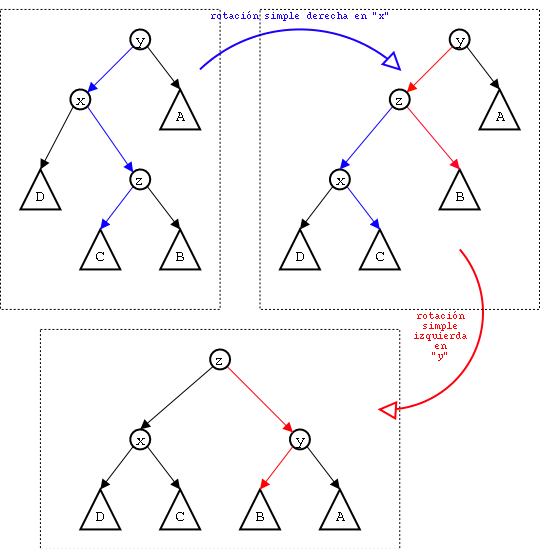
En realidad, la rotación doble constará de dos rotaciones simples. El caso general de la rotación doble izquierda en un árbol AVL se puede observar en Figure 11.
La rotación doble derecha es el proceso inverso a la rotación doble izquierda.
Dado que, como vimos, una rotación doble es en realidad dos rotaciones simples, podemos implementar la función para la rotación doble tan sólo utilizando rotar_s vista en the Section called Implementación de la rotación simple: lo cual se hace a continuación:
void rotar_d (AVLTree ** t, bool izq);/* realiza una rotación doble. Funciona análogamente a rotar_s(). */ void rotar_d (AVLTree ** t, bool izq)
{ if (izq) /* rotación izquierda */ { rotar_s (&(*t)->izq, false); rotar_s (t, true); } else /* rotación derecha */ { rotar_s (&(*t)->der, true); rotar_s (t, false); } /* la actualización de las alturas se realiza en las rotaciones simples */ }

- Declaración de la función rotar_d(); debería ir en un archivo de cabecera.

- Los parámetros de rotar_d() son análogos a los de rotar_s() vistos en the Section called Implementación de la rotación simple:.
Balance del árbol
Como se mostró anteriormente, cda vez que se modifique el árbol (i.e. agreguen o eliminen elementos) corremos el riesgo de que pierda su propiedad de equilibrio en alguno de sus nodos, la cual debe conservarse si queremos obtener tiempos de ejecución de orden O(log(n)) en el peor de los casos.
La idea general que se utiliza en esta implementación de árboles AVL para implementar los algoritmos de inserción y de eliminación de nodos sobre un AVL es la siguiente:
Efectuar los algoritmos de igual forma que en los árboles binarios de búsqueda pero
en cada recursión ir actualizando las alturas y rebalanceando el árbol en caso de que sea necesario.
En the Section called Consideraciones sobre la altura de los nodos se implementó una función de tiempo de ejecución O(log(n)), peor caso, para actualizar la altura de un nodo. Así, lo que nos falta es una función que detecte un "desequilibrio" en un nodo dado del árbol y por medio de un número finito de rotaciones lo equilibre.
Important: No se demostrará aquí, pero cabe señalar la existencia de un teorema que asegura que el número máximo de rotaciones para equilibrar un árbol AVL luego de una inserción es 2 y luego de una eliminación es log(n) dónde n es el número de nodos.
En las secciones anteriores hemos ya descripto a grandes razgos cuál rotación usar en cada caso de desequilibrio. Esperamos que en el código siguiente el lector pueda formalizar tales ideas.
void balancear (AVLTree ** t);/* Detecta y corrige por medio de un número finito de rotaciones un desequilibrio en el árbol *t. Dicho desequilibrio no debe tener una diferencia de alturas de más de 2. */ void balancear (AVLTree ** t) { if(!es_vacio(*t)) { if (altura (izquierdo (*t)) - altura (derecho (*t)) == 2)
{ /* desequilibrio hacia la izquierda! */ if (altura ((*t)->izq->izq) >= altura ((*t)->izq->der))
/* desequilibrio simple hacia la izquierda */ rotar_s (t, true); else /* desequilibrio doble hacia la izquierda */ rotar_d (t, true); } else if (altura (derecho (*t)) - altura (izquierdo (*t)) == 2)
{ /* desequilibrio hacia la derecha! */ if (altura ((*t)->der->der) >= altura ((*t)->der->izq)) /* desequilibrio simple hacia la izquierda */ rotar_s (t, false); else /* desequilibrio doble hacia la izquierda */ rotar_d (t, false); } } }

- Declaración de la función balancear(). Esta declaración junto con el comentario que le sigue deberían estar en un archivo de cabecera usado para la interfaz del tipo abstracto de dato árbol avl con el usuario-programador.

- Como dice en el comentario de la función, sólo se contemplarán aquellos desequilibrios cuya diferencia entre alturas es hasta 2.

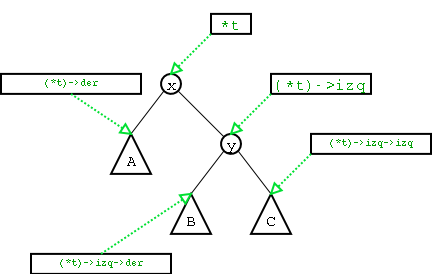
- Sabiendo que en el nodo al que apunta *t hay un desequilibrio hacia la izquierda (de diferencia de alturas 2), debemos averiguar qué clase de rotación aplicar. En Figure 12 se explica gráficamente a dónde apuntan las variables de la función en un árbol genérico.
Como puede verse en el código, nos decidimos por una rotación simple izquierda si el subárbol más pesado de (*t)->izq es el izquierdo o por una rotación doble izquierda si el subárbol más pesado de (*t)->izq es el derecho.

- Si detectamos un desequilibrio hacia la derecha, la toma de deciciones son análogas a las de un desequilibrio hacia la izquierda, las cuales ya explicamos.
Inserción
Como dijimos en the Section called Balance del árbol, implementaremos la inserción de elementos en un árbol AVL de forma análoga a cómo lo haríamos para árboles binarios de búsqueda salvo que en cada recursión del algoritmo verificaremos y corregiremos el equilibrio del árbol. También es importante ir actualizando las alturas de cada nodo en cada recursión dado que las rotaciones, inserciónes y eliminaciones pueden modificarlas.
Dado que ya vimos funciones tanto para balancear un árbol y para actualizar la altura de un nodo (ambas de tiempo de ejecución constante), estamos listos para implementar el algoritmo de inserción. Esperamos que sea intuitivo.
void insertar (AVLTree ** t, int x);
/* inserta x en el árbol en un tiempo O(log(n)) peor caso. */
void
insertar (AVLTree ** t, int x)
{
if (es_vacio (*t))
*t = hacer (x, vacio (), vacio ()); /* altura actualizada
automáticamente */
else
{
if (x < raiz (*t))
insertar (&(*t)->izq, x);
else
insertar (&(*t)->der, x);
balancear (t);
actualizar_altura (*t);
}
}
Eliminación
La estrategia para diseñar el algoritmo de eliminación sobre árboles AVL es la misma que para la inserción: Se utiliza el mismo algoritmo que sobre árboles binarios de búsqueda, pero en cada recursión se detectan y corrijen errores por medio de balancear() y se actualiza la altura del nodo actual.
Recordamos un poco la idea del algoritmo de eliminación sobre árboles binarios de búsqueda. Primero se recorre el árbol para detectar el nodo a eliminar. Una vez hecho esto hay tres casos a diferenciar por su complejidad:
Si dicho nodo es una hoja procedemos a eliminarlos de inmediato, sin más.
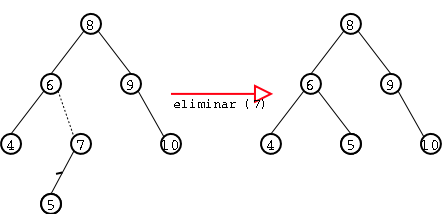
Si dicho nodo tiene un sólo hijo, el nodo puede eliminarse después de ajustar un apuntador del padre para saltar el nodo. Esto se muestra en Figure 13.
Si dicho nodo tiene dos hijos el caso es un poco más complicado. Lo que se estila hacer (y que de hecho se hace en el algoritmo gracias a la función auxiliar eliminar_min()) reemplazar el nodo actual por el menor nodo de su subárbol derecho (y luego eliminar éste).
void eliminar (AVLTree ** t, int x);
/* elimina x del árbol en un tiempo O(log(n)) peor caso.
Precondición: existe un nodo con valor x en el árbol
t. */
int eliminar_min (AVLTree ** t);
/* Función auxiliar a eliminar(). Elimina el menor nodo del árbol
*t devolviendo su contenido (el cual no se libera de
memoria). Se actualizan las alturas de los nodos.
Precondición: !es_vacio(*t) */
void
eliminar (AVLTree ** t, int x)
{
AVLTree *aux;
if (x < raiz (*t))
eliminar (&(*t)->izq, x);
else if (x > raiz (*t))
eliminar (&(*t)->der, x);
else /* coincidencia! */
{
if (es_vacio (izquierdo (*t)) && es_vacio (derecho (*t)))
{/* es una hoja */
free (*t);
(*t) = vacio();
}
else if (es_vacio (izquierdo (*t)))
{/* subárbol izquierdo vacio */
aux = (*t);
(*t) = (*t)->der;
free (aux);
}
else if (es_vacio (derecho (*t)))
{/* subárbol derecho vacio */
aux = (*t);
(*t) = (*t)->izq;
free (aux);
}
else /* caso más complicado */
{
(*t)->dato = eliminar_min (&(*t)->der);
}
}
balancear (t);
actualizar_altura (*t);
}
int
eliminar_min (AVLTree ** t)
{
if (es_vacio (*t))
{
fprintf (stderr,
"No se respeta precondición de eliminar_min()\n");
exit(0);
}
else
{
if (!es_vacio (izquierdo (*t)))
{
int x = eliminar_min (&(*t)->izq);
balancear (t);
actualizar_altura (*t);
return x;
}
else
{
AVLTree *aux = (*t);
int x = raiz (aux);
*t = derecho (*t);
free (aux);
balancear (t);
actualizar_altura (*t);
return x;
}
}
}
Conclusión
No realizada aún.
Performance
No realizada aún. Hacer: comparaciones de tiempos con otros TADs similares (ABB, Heaps, linkedlists, etc).
Bibliography
A. GNU Free Documentation License
GNU Free Documentation License Version 1.2, November 2002
Copyright (C) 2000,2001,2002 Free Software Foundation, Inc.
59 Temple Place, Suite 330, Boston, MA 02111-1307 USA Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
State on the Title page the name of the publisher of the Modified Version, as the publisher.
Preserve all the copyright notices of the Document.
Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
Include an unaltered copy of this License.
Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
Delete any section Entitled "Endorsements". Such a section may not be included in the Modified Version.
Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties--for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided for under this License. Any other attempt to copy, modify, sublicense or distribute the Document is void, and will automatically terminate your rights under this License. However, parties who have received copies, or rights, from you under this License will not have their licenses terminated so long as such parties remain in full compliance.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation.
ADDENDUM: How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
Copyright (c) YEAR YOUR NAME. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
with the Invariant Sections being LIST THEIR TITLES, with the Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.