POVRAY III: Yinelemeli Yapıların Tasarımı

ArticleCategory: [Choose a category for your article]

AuthorImage:[Here we need a little image from you]

TranslationInfo:[Author and translation history]

original in es Antonio Castro 

es to en Miguel A Sepulveda

en to tr Özgür Ulaş Kırlangıç

AboutTheAuthor:[A small biography about the author]

Abstract:[Here you write a little summary]

ArticleIllustration:[This is the title picture for your article]

ArticleBody:[The article body]

Bilgisayar Biliminde Sanat ve Teknik.

Basit Geometrik Objeler

• Küre
  syntax: sphere { < x, y, z>, radius ... }
  burada x, y, z merkezin koordinatlarıdır. Yarıçap'ı (radius) diğer özellikleri de belirtmek için ölçek (scale), dönme (rotation), ilerleme (translation), doku (texture), renk (color), vb. ek parametreler izleyebilir.
• Koni
  syntax: cone { <x1, y1, z1>, rad1 <x2, y2, z2>, rad2 [open] ..... }
  Bu ifade bir uçtaki koni merkezi koordinatları x1,y1,z1 ve kesitteki yarıçapı r1 olan ve diğer uçtaki merkez koordinatları x2,y2,z2 ve yarıçapı r2 olan bir koni belirtmemize izin verir. Tam koni oluşturmak için sadece yarıçaplardan birini sıfır yapın. Diğer bir seçimlik (optional) parametre de verildiği zaman açık, verilmediği zaman kapalı bir koni render eden "open" simgesidir (token).
• Silindir
  syntax:cylinder { <x1, y1, z1>, <x2, y2, z2>, rad [open] ...... }
  burada x1, y1, z1 ve x2, y2, z2 silindirin her iki ucundaki merkez koordinatlarıdır. Önceki gibi rad silindir kesiti yarıçapıdır ve "open" simgesi (token) ise açık veya kapalı (eğer verilmemişse) silindir seçen seçimlik parametredir.
  
• Düzlem
  syntax:plane { <x, y, z>, dist ..... }
  Bu defa x, y, z bir noktanın koordinatları yerine bir düzlemin yüzeyine dik olan vektörü temsil ederler. dist değeri ise koordinat merkezinden düzleme olan uzaklıktır. Hatırlayın Povray vektörlerin kısaltma şeklinde gösterimine izin vermektedir. x = <0, 1 , 0> -z = <0, 0, -1>. Bazen bir düzlem çok büyük yarıçaplı bir küre kullanılarak gösterilebilir; aslında bu tekniği önceki makalelerimizden birinde kullanmıştık.
• Kutu
  syntax: box { <x1, y1, z1>, <x2, y2, z2>...... }
  burada x1, y1, z1 ve x2. y2. z2 kutunun karşıt köse koordinatlarıdır

Koşullu Katı Grafiği (CSG)

CGS ilkelleri daha komplike modeller oluşturmak için birleştirilebilen temel katı objelerdir. Son kombinasyon guruplandırılabilir ve ölçekleme (scaling), ilerletmeler (translations), döndürmeler (rotations) veya doku ile doldurmalar (filling in textures), vb... kullanılarak dönüştürülebilir. Bu dönüştürmelerin her birini, bileşik model içindeki herbir ve tüm temel ilkellere uygulamak şart değildir.

CGS ilkellerini birleştiren dört ayrı method ile tekil ilkellere uygulanan beşinci bir tamamayıcı metod mevcuttur:

• Birleşim
  'union { object {A} object{B} }'
  Birleşik objedeki noktaların tümü A VEYA B'ye aittir.
• Kesişim
  'intersection { object {A} object {B} }'
  Birleşik objedeki noktaların tümü A VE B'ye aittir.
• Tersi
  object {A inverse}
  Birleşik objedeki noktaların tümü A'ya ait olmayan noktalardır.
• Fark
  'difference { object {A} object {B} }'
  Birleşik objedeki noktaların tümü A'ya ait olup B'ye ait olmayan noktalardır,
  diğer bir değişle 'union { object {A} object {B inverse }'
• Ekle
  'merge { object {A} object {B} }'

  A ve B'nin iç yüzeylerinin kaldırılması hariç Birleşim methodu gibidir. Eğer objeler yarısaydam (translucid) değillerse bu özelliğin kullanımı gereksizdir.

Takip eden örneklerde katı modeller oluşturmak için bu işlemlerden birkaçını kullanacağız. Model oluştururken öncelikle toplam hacmi oluşturmak için gerekli olan tüm elemanları eklemeyi sonra da istenmeyen parçalardan kurtulmak için kesişim işlemlerini kullanmayı tavsiye ederim.

 
#define EatenApple = intersection { 
      object { WholeApple } 
      object { Bite1 inverse } 
      object { Bite2 inverse } 
} 
 

Bir katı modeldeki ilkel objelerin ortak yüzeyleri varsa yüzeylerden biri üzerindeki noktaların render edilmesinde makine hassasiyetine bağlı probemler olabilir. Bu problem yüzeyin hangi objeye ait olduğunu net bir şekilde ayırd etmek için objelerden birine çok küçük bir yer değiştirme vermek suretiyle giderilebilir.

Povray içinde Döngüler ve Koşullamalar.

Bir görüntü içindeki elemanlar genellikle rastlantısal bir sıralama ile tanımlanırlar. Bununla beraber, yenilemeli yapılar yaratmak için örneğin, prosedür döngüleri uygulamanın çok elverişli olduğu durumlar mevcuttur. Povray içinde döngüler çeşitli metodlar kullanılarak uygulanabilirler. Bir metod dilin kendisi tarafından sağlanan döngü akış kontrol direktifidir (loop flow control directive).

Döngü akış kontrolü POVRAY programlama arayüzünün birçok direktifinden sadece biridir. Bir süre önce #declare ve #include gibi başka direktiflerden bahsetmiş ve diğer birçoğunu ikinci derecede önemli olarak karakterize etmiştik. Takip eden örnek direkt olarak POVRAY içinde düzenlendi ve itiraf etmeliyim ki bu benim döngü akış kontrol direktifini ilk kullanışım. Bunun sebebi, genellikle döngü akış kontrol ifadelerine (for döngüsü) sahip harici bir program (C veya C++) ile POVRAY kaynağı oluşturarak aynı sonucu elde etmenin mümkün olmasıdır. İleride bu teknik için bir örnek göreceğiz.

C tecrübesi olan okuyucular, Povray'in programlama arayüzünün diğer genel amaçlı programlama dillerinde (C, C++) olduğu kadar mükemmel olmadığını göreceklerdir. Bu bir sürpriz olarak gelmemeli çünkü POVRAY görüntü tanımlamak üzere taraslanmış bir dildir, ve akış kontrol direktifleri sonradan yapılmış eklenmelerdir. Benzer şekilde, POVRAY karmaşık matematiksel işlemleri gerçekleştirmek için gerekli direktifler ile her türlü döngüyü de içermektedir. Kişisel olarak POVRAY'in tüm bu işlemleri barındırıyor olmasını inanılmaz buluyorum fakat diğer yandan aslına bakılırsa ille de gerekli olduklarını düşünmüyorum, çünkü bu işlemleri daha güçlü programlama dilleri içerisinde harici olarak gördürmemiz herzaman mümkün. Bu işlemleri dışarıda veya içeride gerçekleştirmenin kompozisyonun nihai sanatsal değeri üzerinde ne tür bir farklılık yaratacağını düşünemiyorum. Benim için en önemli konu nihai resmin kalitesidir. Daha dar bir kapsamda görüntüyü tasarlayıp ve proses etmek için gereken zaman ve uğraş da bir faktör olmalı. Genel amaçlı programlama dillerine daha fazla aşina olan kullanıcılar POVRAY dosyalarını onlar üzerinden oluştururken kendilerini daha iyi hissedebilirler, programlama tecrübesi olmayan diğerleri ise belkide direkt olarak POVRAY üzerinde yazarken daha rahat edebilirler. Ayrıca basit resimler için POVRAY içinde direkt düzenleme daha kolay olurken kompleks görüntüler için POVRAY dosyalarının diğer programlarla oluşturulması daha iyi olabilir. Her iki metodu da inceleyeceğiz ve okuyucunun bu bağlamda seçim yapmasına olanak tanıyacağız.

Deneme Yanılma Metodu Kullanmak

Birçok görüntü basit bir fikirden yola çıkarak tasarlanabilir. İlk uygulamadan sonra daha iyi bir sonuç elde edebilmek için bazı değerleri değiştirmeye veya yaklaşık değerler kullanmaya karar verebiliriz. Yani deneme yanılma metodu POVRAY içerisinde görüntü tasarımı yapma işinin önemli bir parçadır. Bu makaleler serisinin başlangıcında okuyuculara resim oluşturulmayı kolaylaştıran basit bir script-tool (POV) önermiştik, fakat okuyucu bu küçük script'in yeterli olduğunu düşünmemeli. Çoğu zaman çizgisiz kağıt, kalem ve bir hesap makinesine ihtiyacınız olacak. Bir çok durumda tasarımlarımız 3-Boyutlu geometriler içerdiğinden, bazı efektleri elde edebilmek için başka yolu yok bir miktar özel geometri ve trigonometri bilgisi olmazsa olmaz. Genellikle birkaç formülü bilmek yeterlidir, bu nedenle bazı temel trigonometrik bağıntıları hatırlayalım:

Yani:

Sonraki hatırlatma olarak trigonometrik fonkyonların ana tanım kümelerini kuadrantın bir fonksyonu olarak tablolaştırıyoruz:

Bu son ilişki tek (unique) olarak tanımlı değil. Alfa açısı +/- 180 dereceler için belirsiz (undetermined). Hesaplama yönünden şunu kullanmak tercih edilir:

Sonuç olarak P1(x1,y1,z1)'den P2(x2,y2,z2)'ye olan mesafe

D = sqrt( (x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2 )

Daha birçok kullanışlı trigonometrik bağıntı var fakat gözden geçirdiklerimiz birçok durum için yeterli olacaktır. POVRAY içerisinde kullanılan trigonometrik fonksyonlar açıların radyandan cinsinden verileceğini varsayarlar. Dönüşüm fonksyonu radians(alfa) dereceyi radyana çevirir. Ne yazık ki POVRAY tutarlı değil, örneğin dönmeler (rotations) derece cinsinden ölçülmektedir :-(

Deniz Kestaneleri

Bu örnekte bir miktar temel trigonometri kullanıyoruz. Deniz kestanelerinde iğneler öyle düzgün bir şekilde yerleştirilmişlerdir ki bu etkiyi şansa bağlı olarak elde etmek kolay olmasa gerek. Tasarımcı iğneleri kesin olarak yerleştirmek için bir algortma düşünmeli ve bunu nihai 3 boyutlu konfigurasyonun net tasavvuru ile uygulamalı. Bu örneğin kaynak kodu gerektiği şekilde belgelendi, bu nedenle burada daha fazla yorum yapmanın bir faydası yok. Bu örnek bir döngü algoritmasının işe yaradığı net bir durum. Kullanıcının döngüyü POVRAY içerisinde veya dışarıda bir C-programı üzerinde uygulamaya karar vermesi kişisel tercih meselesidir.

Balikların kaynakları da burda. Bunlar daha önce bahsedildiği gibi CGS ilkelleri kullanılarak modellendiler.

Sırada geri kalan görüntünün kaynakları var. Buradaki en özel iş hiç şüphesiz ki kompozisyndaki başlıca karakterler olan deniz kestanelerinin (ispanyolcası erizo) tanımı:

Bu örnek içerisindeki birkaç efekt tamamiyle yeni, mesela kum üzerindeki yüzey efektleri (kum üzerindeki dalgalar), atmosferik efektler (yeşil deniz renginde çok kalın ve çok nemli bir sis) ve pek tabiki karmaşık CGS objeleri. Yüzeydeki dalgalardan serpilen düzensizlik ile karakterize olmuş görüntüdeki ışık birçok noktasal kaynaktan gelmekte, deniz altı aydınlanmasını simule etmek için ortamda dağılmakta. Bu kompozisyon için tek bir ışık kaynağı uygun olmazdı çünkü bu deniz kestanesinin gölgesinin çok keskin olmasına sebep olurdu.

Harici Programlar ile Üretim

Bir ray-tracer yalnızca formal bir rey-tracing dili yardımı ile tanımlanmış olan görüntüyü oluşturmada kullanılan için bir araçtır. Rey-tracer'lar renk ve ışık vb... tanımlamaları algılayabilirler. Çoğu zaman tasarım işimizi desekleyecek ön çalışmalar vardır: 3-Boyutlu tarayıcılar, format dönüştürme araçları, programlar, bunlar arasında sayılabilir. Öyleyse bir ray-tracer, görüntü inşa ve tasarım araçları zincirinde halkalardan yalnızca biridir. Diğer bir söyleyişle düşüncelerimizi klavyeye dökerek tasarım yapmak sanatsal kompozizyonlar üretmek için tek mekanizma değildir, elle bir ray-tracer dilinde yazmanın çok kolay olmadığı daha karmaşık kompozisyonları üretmek için yardımcı araçlarımız mevcuttur.

Harici bir program ile oluşturulmuş karmaşık bir görüntü örneği olarak sırada bir burbujaz.c (baloncuklar) adında bir C-programı veriyoruz. Program 1000x750 piksel boyutundaki bir yüzey üzerine rastlantısal olarak baloncuklar yerleştiriyor. Baloncuklar birbirleri ile kesişemiyorlar, bu nedenle örnek kodumuz raslantısal yerleri ve raslantısal boyutları bu koşula göre belirliyor. Eğer bir baloncuk için oluşturulan yeni konum var olan diğer bir balonun yanına düşüyorsa yeni bir konum hesaplanıyor. Kürenin boyutu uygun olacak şekilde küçültülüyor. Çok sayıda iterasyon ardından hemen hemen hiç boş yer kalmamış bir yüzey elde ediliyor. Bu özel örneğin oluşturulması çok sayıda hesaplama gerektiriyor çünkü seri ilerledikçe yeni bir baloncuğu uydurmak daha da zor olmaya başlıyor.

Bu programı derleyin ve çalıştırın. Standard çıktıyı baloncuklar için verilerin saklandığı 'burbujas.inc' adında bir dosyaya yönlendirin (burbujas > burbujas.inc). Çıktı dosyası aşağıdakine benzer satırlar içerecektir:

 
sphere{<-375, 0,   33> 55.0000000 texture{Gold_Metal}} //(0/1) 
sphere{< -86, 0,   62> 55.0000000 texture{Gold_Metal}} //(1/2) 
sphere{<-326, 0,  346> 55.0000000 texture{Gold_Metal}} //(2/3) 
sphere{< 190, 0, -156> 55.0000000 texture{Gold_Metal}} //(3/4) 
sphere{<  62, 0, -293> 55.0000000 texture{Gold_Metal}} //(4/5) 
sphere{< 323, 0,  161> 55.0000000 texture{Gold_Metal}} //(5/6) 
sphere{< 341, 0,  -15> 55.0000000 texture{Gold_Metal}} //(6/7) 
................... 

Biraz sabır öneririm çünkü çıktı dosyasının oluşturulması biraz zaman alıyor. Herhangi bir anda işlemi durdurabilir ve son çıktı satırını düzenleyerek tamamlanmış hale getirebilirsiniz. Veya eksik satırı dosyadan çıkarın. Pov için kaynak aşağıdaki gibi olacaktır:

Kaynak kodu gene "clock" simgesine atıflar içeriyor fakat bu sefer amacı çok farklı. Bu defa bir animasyon için resimler serisi üretmek yerine çok farklı görüntü noktası olan 4 resim üretiyor. Kamera pozisyonu, açısı ve açıklığı (aperture) dört resim için de farklı.

Bir önceki POVRAY makalesinde bir noktada POVRAY içerisinde kamera olanaklarını inceleyen örnekler inceleyecebileceğimizi belirtmiştik. İşte bu bir örnek. Kamera tanımlamalarına bağlı olarak render edilmiş nihai resimler üzerindeki farklar hayli belirgin. Açıklık (aperture) açısına bağlı olarak çok farklı pespektifler elde edilebilir: Küçük açı uzak perspektifleri verirken, geniş açılar yakın perspektifleri sunar. En geniş açıklık 180 derecedir, bu çok uç bir değerdir çünkü şekilleri ayırt etmek zordur.

Gösterilen resimler bir Pentium 200 MMX 48 MB Ram (398 bogomips) üzerinde preses edildiler. Önerildiği gibi önceki serilerde verilimiş olan 'pov' aracı kullanılarak çalıştırıdı:

Geçilen parametreler şunları temsil ederler:

• Kaynak dosyası (Source file) burbujas.pov'dur
• Boyut(Size) 6 = (400x300)
• Kalite (Quality) 9
• Başlangıç fotogramı (Initial photogram) = 1
• Bitiş fotogramı (Final photogram) = 5
• Başlangıç saati (Initial clock) = 1
• Bitiş saati (Final clock) = 5

Herbir fotogramın oluşturulması için harcanan zaman kaydadeğer. Daha iyi bir kalite ile aşağıdaki zamanları alırdı:

Şimdi sonuçları inceleyelim. Dört fotogramdan ilkinde tek değişiklik kamera kurgusunda. (poziston (position), açı (angle), yönlendirme (orientation) v.b.)

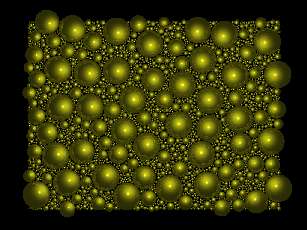
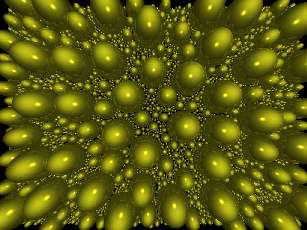
Son fotogramı göstermeden önce bu son resmin değerini arttırma ile alakalı diğer bir konu üzerinden gitmeme izin verin, CPU optimizasyonu konusu.

CPU Kullanımı Optimizasyonu

Son program en karmaşık olanı idi ve POVRAY onu optimize etmeyi başaramadı. Karmaşık kompozisyonlarla karşı karşıya kaldığında ray-tracer görüntüyü en basit ortak paydaya sadeleştirmeye çalışır. POVRAY'in önceki versyonlarında optimizasyonların elle yapılması zorunluydu; sanatçıların bir veya daha fazla objeyi örtecek bir ilkeli tanımlamak için "bounded_by" direktifleri vardı. Ray-tracer bu örtünme ile çarpışmayan ışınların içerideki objeler ile de çarpışmayacağını farz ediyordu. Bu bir miktar proses zamanı kazandıran bir yaklaşımdır (approximation). Hakikaten işe yaradığı durumlar ise çok nadirdir. Sonuçlarına bakılırsa son resmimiz bu durumlardan biri! Son görüntü çok fazla resim içeriyor ve çok karmaşık. Bu nedenle kompozisyonu el yordamıyla optimize etmek daha iyi olabilirdi, örneğin baloncukları bölge bölge gruplamak, baloncukları bileşik objeler halinde birleştirmek veya hatta "bounde_by" komutu ile aynı bölgeleri küre gruplarını örtüp tüm baloncukları bir obje halinde birleştirmek. Sentaks şöyle olurdu:

 
    union { 
    sphere { <x1, y1, z1>, r1 }  
    sphere { <x2, y2, z2>, r1 } 
    sphere { <x3, y3, z3>, r1 } 
    .......................... 
    bounded_by { sphere { <xb, yb, zb>, rb } } 
  } 

Açıklanan türdeki el yordamı optimizasyon birleşimlerle ve kesişmelerle ve hatta herhangi bir diğer obje ile kullanılabilir. Kullanıcı başka örtme ilkellerini de seçebilir, biz bir küre seçtik, fakat en iyi sonuçlar genellikle kutular ve kürelerle elde edilmekte. Eğer seçilen ilkel birleşik objenin bir parçasını dışarıda bırakılırsa sonuç arızalı olabilir.

Bir kere daha vurgulamak isterim ki el yordamı optimizasyonlara nadiren ihtiyaç duyulur. Son örneğimiz konuyu açmak için önceden 'kötü niyetle' tasarlanmıştı. POVRAY otomatik eniyileyicisi kompozisyonu daha iyi bir hale getirmeyi beceremedi. Kompozisyon 2154 küre içeriyor. Okuyucu bu sayıyı sayarak kontrol edebilir :-).

Örneğimizde ray-tracer'ın olanakları ile nasıl oynanacağını gösterdik. Çoğu zaman aynı düşünce veya kavram farklı sonuçlar elde etmek için değişik şekillerde uygulanabilir ve burası sanatçının yaratıcılığının su yüzüne çıktığı yerdir.

Eksik olan...

Povray bazıları daha az veya daha çok ilginç olan birçok matematik fonksyonu sunuyor. Fakat ne yazık ki çok ilginç bir fonksyon eksik. "spline" fonksyonu. Bir kalem ile kağıta birkaç nokta işaretledikten sonra noktaların üzerinden yumuşak bir çizgi ile geçen bir fonksyon uygulaması kadar kullanışlı birşey yoktur. Povray'in spline ilkeli bir fonksyon olarak kullanılamaz, bunun yerine diğer formların inşasında baz olacak bir çizgi oluşturur, eğer spline'ı istediğimiz tüm değişkenlere uygulayabilseydik ne iyi olurdu. Bu, örneğin bir kameranın keyfi bir yörünge izlemesini olanaklı kılardı. Eğer harici fonsyonları uygulayabilseydik de çok iyi olurdu. Bir seviyeye kadar tüm bunlar include kullanarak ve harici programlama yaparak elde edilebilir. Linux altında 'spline' adı altında bir araç (utility) var. Bu, bir noktalar kümesinden istenilen eğriyi oluşturan bir komut olarak kullanılabilir. Bu komutu harici programlama ile kullanmayı deneyin, örneğin animasyonlar veya kamera hareketi oluşturmak için.

Egzersizler

• En son verilen tavsiyeleri izleyerek son fotogramı optimize edin.
• burbujas.c programını POVRAY diline tercüme edin.
• erizos.c programını genel amaçlı bir dile tercüme edin.

Okuyucu katkıları

Okuyuculardan haber almayı ve kompozisyonlarını (belki de burada tartışılan yinelemeli veya döngü yapılarını uyguladıkları) görmeyi çok isterim. Lütfen deneylerinizi sıkıştırılmış dosyalar içinde gönderin. Okuyucu katkılarını biriktirmek ve burada LinuxFocus dergisinde bir sergi organize etmek harika olurdu. Sergi için en ilginç veya yaratıcı olan resimleri seçeceğim. Lütfen herhangi bir ticari ödeme-karşılığı lisansı (for-pay license) altındaki resimleri göndermeyin. Eğer mümkünse resimlerinizin kaynaklarını da gönderin ki diğer insanlar da sizin fikirlerinizden birşeyler öğrenebilsin.

Kaynakça

• Povray ana sayfası: http://www.povray.org.
• Önceki makaleler: Povray I: The first steps I
  POVRAY II: Basic notions
  
• Bu makale için kaynak kod : pov3.tar.gz (40 Kb)
• Bu makalede kullanılan povray versyonu 3.1g idi. Bu versyon, yazının yazıldığı tarihte www.povray.org adresinde mevcut olan güncel versyondu. Siz de aynı şekilde onları _LF_ sunucusundan indirebilirsiniz: pre-compiled: povlinux.tgz (1.4Mb), unix sources: povuni_s.tgz (960Kb).